When it comes to writing, reviewing, and proofreading scientific publications and text books (for university students), I am convinced that a radical wisdom of the crowd paradigm does not apply, mostly because the crowds are too small and likely also too fragmented. However, the principles of open access definitely allow larger communities to contribute suggestions, ideas, and corrections to publications, simply because the hurdles and the fuss brought about by copyright restrictions are removed. In this post, I propose that there is much more potential to unleash for the writing and editing process by borrowing concepts and adopting technologies from open source software development.

1. Motivation

The motivation behind the ideas presented here comes from my experience with the almost completed process of creating the second edition of my introduction to German grammar (Einführung in die grammatische Beschreibung des Deutschen) published by Language Science Press. The second edition was necessary because of many minor errata and my dissatisfaction with the chapter on phonology. After the first edition had been published, I first created a traditional list of errata (now removed) on the book’s website. The process of tracking errata typically involved colleagues writing me an email, telling me things like which word was misspelled on which page. I would then log in to the book’s WordPress site and make an entry in an unstructured list. This is the same workflow that was used in 1900, except that back then emails were letters to authors or editors, and book websites were printed sheets added to (or even glued to the inside of the book cover of) the remaining copies of the current edition. This workflow – intended to eradicate errors – is itself prone to introducing errors, mostly because information is copied by humans in several places. Even worse, having to write a personal email to the author involves a high inhibition threshold and an unreasonably high workload given the amount of transmitted information. Also, there is no automatic way of keeping track of which errors have already been fixed and which haven’t. Most severely for the readers, however, they have to either go to a website and check whether a potential erratum has already been recognized as an erratum, or simply wait for the next edition. If it is a substantial error and not just a typo, it would be favorable to implement the fix as quickly as possible and deploy a fixed version to the reader. In summary, traditional lists of errata and the traditional editing processes are laborious, error-prone, and clumsy.

The open review of Stefan Müller’s Grammatical Theory has demonstrated to the linguistics community that open processes in publishing actually do work. Using the hypothes.is platform has shown that the technology to implement the new open processes is already there. In a recent post, Stefan describes how community proofreading helped to polish his Grammatical Theory using contributions from the larger community and the hypothes.is platform. I suggest that also after a book’s release, we should adopt community-based efficient and modern workflows from open source software development for tracking errors and creating new editions. Using platforms like GitHub, open source software developers have efficient ways of

• checking the daily updated state of the work done by other programmers
• reporting errors with precise reference to the software version and even source code line numbers where the errors are located
• having bi-channel discussions of errors or suggestions and the optimal way to fix or implement them – or why they are rejected
• keeping track of what has been fixed and what hasn’t
• differentiating between major releases (“editions” in publishing parlance) and minor releases which merely fix errors and don’t change the intended behavior of the product

How could it not be desirable to use similar methods in open access publishing?

2. How it can be done

I will now briefly go through some methods that we as authors, editors, and readers of open access books can use, and what benefit they bring about. As a paradigm, I refer to them as open authoring. The two key technologies to be used are version control and issue tracking. Based on these technologies, we replace traditional editions by milestones, releases, branches, and forks.

2.1 Version control

Version control systems keep track of all changes made to code by developers – in our case to text written by authors – much like a persistent and collaborative undo function. In open authoring projects, the history of edits is visible publicly, while only registered authors can actually make changes. At Language Science Press, the LaTeX code of all books is checked into the version control repository GitHub. After Language Science Press had checked in my German grammar book, I actually used GitHub for working on the second edition. Everybody can see, for example, which changes I made (and when) to the chapter on Phonology (just click the link). Typically, at the end of the day, I would commit my changes into the repository and upload (push) them to GitHub. Such detailed information on the editing history is the backbone of open authoring.

2.2 Issue tracking

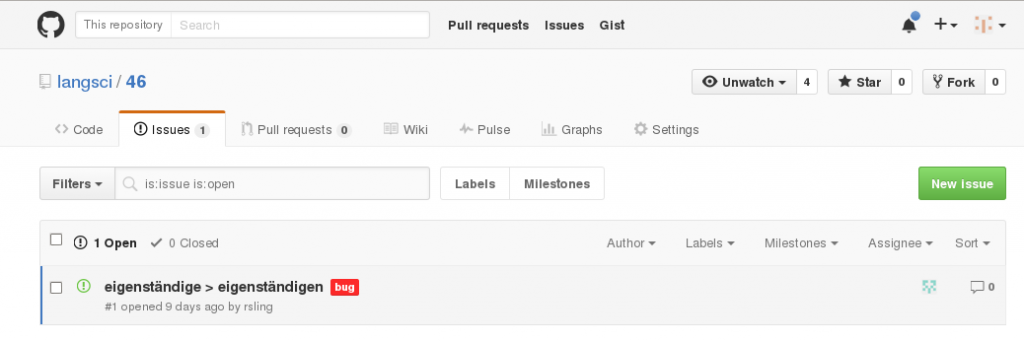
The interactive aspects come into play with issue tracking, also available on platforms like GitHub. Instead of emailing an author about an erratum, readers (and authors, of course) simply open an issue (sometimes called a ticket), which is a description of the error and where it occurs that is stored and maintained (in a structured way) on GitHub. Other readers, as well as the authors and editors, can view the issues and comment or discuss them publicly. I have not used the issue tracker for my grammar book yet, but I have created a sample entry for illustration purposes here: https://github.com/langsci/46/issues/1.

Submitting an issue for a typo in EGBD

You can click on the link in the issue’s first comment in order to jump directly to the line in the LaTeX code where the error occurs. Of course, issues are not restricted to errors. Maintainers of repositories can create appropriate categories themselves, for example requests (e.g., for a more detailed explanation of some linguistic notion), suggestions or questions. The issue tracker has the necessary functionality for discussing the issue and marking its status as assigned (to a particular author), solved, rejected, etc.

2.3 Milestones, releases, and branches

CC-BY-SA Doris Antony

With such a technology in place, we can easily overcome the traditional slow and clumsy release cycle of books described in Section 1. Open source – and consequently open authoring – projects are often organized in milestones, releases, and branches. I now discuss their place in open authoring. Milestones are goals defined by authors as a set of issues that should be fixed. Authors name a list of reported issues (errata, requests, suggestions, questions as mentioned in Section 2.2) which should be resolved at a certain point in time. If an issue tracker is used, the milestones is reached automatically when all issues associated with the milestone are marked as closed (solved or rejected). After reaching a milestone, it makes sense to create a release, which corresponds to an edition in traditional publishing. Releases go into long-term archiving by libraries etc. GitHub is already integrated with Zenodo, which means that a DOI can be created automatically for releases. I see it as an advantage that not all issues need to be addressed for a release. For example, major rewrites can be postponed to later milestones/releases/editions while most authors would probably prefer to have virtually all known typos and factual errors fixed in a release.

Versioning makes all changes and all intermediate versions traceable, no matter how small an incremental the changes are. However, the time between releases is measured in years, and not much is gained if readers only see major releases. As I argued in Section 1, it is desirable to bring intermediate versions to the reader as quickly as possible in order to reduce friction caused by errors of all sort. However, when larger parts of the book are undergoing major rewrites, there are often phases where passages are unfinished, broken, inconsistent, and full of new errors. It is highly undesirable to confront readers with such versions. This is where branching and merging come into play. Branches are separately maintained versions of a publication. In the stable branch, errors are fixed, but no major rewrites take place. It corresponds to the current edition of a book, but with errata fixed incrementally (instead of listed on a piece of paper or a website). In development branches, rewrites take place, which are merged into the stable branch when they have been completed. Development branches are not intended for the general audience but rather for authors, editors, reviewers, etc. In version control systems, branching and merging are standard operations aided by software routines.

2.4 Forks

Another concept known from software projects is forking. In a recent blog post (in German) on grammatick.de, I actually suggested a fork of my grammar book. As a text book, it’s too long for many courses taught at German universities. Therefore, I intend to fork it into a shorter version. Like a branch, a fork is a copy of a project, but the copy is created without the intent of a later merge. Using the second edition (i.e., a release) of my book as a point of departure, I will create a new, shorter book and maintain both books separately. But there is no need to stop there! Because everything is open access, other authors are invited to create their own forks. For example, if some people like the syntax part of my book, they might fork just that part and add more theoretically oriented chapters – or maybe fork those from Stefan Müller’s Grammatical Theory or any other text book that follows both open access and open authoring principles. The CC-BY license already allows for such forks.

2.5 Turning readers into co-authors

Personally, I would embrace yet another consequence of a new open authoring paradigm. With the high level of involvement of readers (students and colleagues) in open authoring, readers can easily become co-authors.

Readers’ comments can greatly improve the quality of a work. CC-BY-NC-ND Matt Zhang.

Up until now, many people contribute to publishing books who don’t receive appropriate credit. The best example are reviewers under the blind review paradigm. As a blind reviewer, you can claim that you reviewed for renowned publisher X, but your name will not be associated with the specific publication which you spent many hours reviewing. The open review paradigm solves this problem. However, while colleagues and students are usually rewarded for comments in the form of enthusiastic thankyous in the preface of books, this can hardly be called proper credit. After all, some of them sacrifice even more of their time than reviewers! Platforms like GitHub offer detailed statistics on the amount of work that people have invested into a project. For example, these graphs on GitHub show who contributed what to my book, and when. I will be happy to accept co-authors! Even if I will probably (but not necessarily) remain the main author, these co-authors will receive credit based on the measured number of changes they contribute to the book.

3. Problems and outlook

There are, of course, some hurdles and obstacles to overcome. First of all, it is clear how everything said here applies to text books. It is, however, not clear whether it makes sense to use open authoring for monographs, edited volumes, or even journal and proceedings papers. Researchers who write traditional monographs usually have little interest in creating a second edition because a completely new book looks much better in their lists of publications. In an ideal world, however, changes to theories and empirical work should be gradual and incremental. Wait! This allows me to make another connection to software development: read the Wikipedia article on iterative and incremental development. This would mean a major change in how the scientific community rewards published results. But why not?

For papers in edited volumes, journals and proceedings, matters are much clearer. Open review is highly appropriate but for such shorter texts, open authoring would most likely not pay off substantially.

One problem I recently learned about is the ISBN system. For each edition, new ISBNs are issued, and the system is not flexible enough to allow for minor updates (i.e., maintenance releases of a stable branch). This just goes to prove that the ISBN system is not adequate for modern publication paradigms. We can of course publish releases under ISBNs but work with incrementally updated versions of books, which would effectively render the ISBN system irrelevant over time. The appropriate identifiers in open and electronic publishing are DOIs or digital object identifiers, anyway. DOIs persistently and uniquely identify all sorts of resources, and they also include information about the location of the resource. Thus, they go beyond ISBNs and ISSNs. As mentioned in Section 2.3, DOIs can be created automatically from GitHub via Zenodo.

A more serious practical problem are page numbers. They would most certainly change a lot from incremental update to incremental update. However, for e-book readers with page reflow, we need a new way of referencing passages from books, anyway. Technically, it is easy to reference letters, words, paragraphs, subsections and sections. Most of this comes for free with publications authored in LaTeX, with some minor technicalities remaining to be solved. In principle, we just have to pick the most practical unit of reference.

The real challenge is getting acceptance for open authoring from the community. First of all, many authors of text books make money by publishing new editions on an annual or bi-annual basis. Most of them will not be interested in open access and open authoring. I don’t intend to morally judge anyone, but making money by selling text books to the weakest in the academic business (i.e., students) is clearly not my preferred model. By extension, this is also true for teaching materials in primary and secondary education – even more so with developing countries in mind. The solution is simple: If we publish enough high-quality open access text books, expensive text books will become less and less attractive. Along the same lines, open educational resources (OERs) are the way to go in primary and secondary education.

Since we’re talking about acceptance, we might as well be blunt. For open authoring to work effectively, authors are required to learn how to use LaTeX (or at least advanced mark-down), version control tools, and issue trackers. Using such tools is a natural thing for software developers, physicists, etc. However, researchers from less technically oriented fields might think that it’s just not worth the trouble. I have no easy solution to offer, and we would all have our fair share of convincing to do. For example, Language Science Press endorses the use of Overleaf, a platform which facilitates writing LaTeX documents collaboratively (see the information for authors by Language Science Press). Like many, I can only say that I have never regretted the time I invested into learning LaTeX, version control, etc.

Using Overleaf for “The empirical base of linguistics”

The good news is that for readers who wish to contribute by reporting errors and making suggestions, we can make things very easy. The manual creation of issues in a tracker surely represents too high a threshold. Instead, we have to create interfaces between tools like hypothes.is as already used by Language Science Press and issue trackers like the one available at GitHub. Ideally, readers should be able to add comments to PDF versions of a book graphically and online (like in hypothes.is). These comments can be converted automatically to issues on GitHub. If the PDF is compiled with SyncTeX enabled, we can even automatically provide references to the lines in the source code alongside the reported issue, just like in my GitHub demo issue. As far as I can tell, this bridging technology is not available yet, however.

To sum up, I argue for taking open access to a new level by using concepts and tools from open source software development under the open authoring paradigm, at least for some types of publications. Deeply involving readers into the (semi-automated and structured) editing process benefits everybody and leads to higher quality publications. The overhead for authors and co-authors is modest and more than compensated for by the benefits. For readers and minor contributors, things even get easier! Most importantly, everybody receives fair credit for the work they contribute to a publication. Most of the necessary technology is already in place thanks to the open source world and platforms like hypothes.is and Zenodo.

What do you think? Please comment or blog about the ideas presented here. Or tweet about #openauthoring to @codeslapper. You can also send me an email to roland.schaefer [email address character] fu-berlin.de, but why not have a totally open discussion about openness?